Singapore sẽ tổ chức một cuộc đua xe Công Thức 1 vào năm 2008. Trước khi cuộc đua diễn ra, đã xuất hiện một số cuộc đua về đêm trái luật. Chính quyền muốn thiết kế một hệ thống kiểm soát giao thông để bắt giữ các tay đua phạm luật. Hệ thống bao gồm một số camera đặt trên các tuyến đường khác nhau. Để đảm bảo tính hiệu quả cho hệ thống, cần có ít nhất một camera dọc theo mỗi vòng đua.

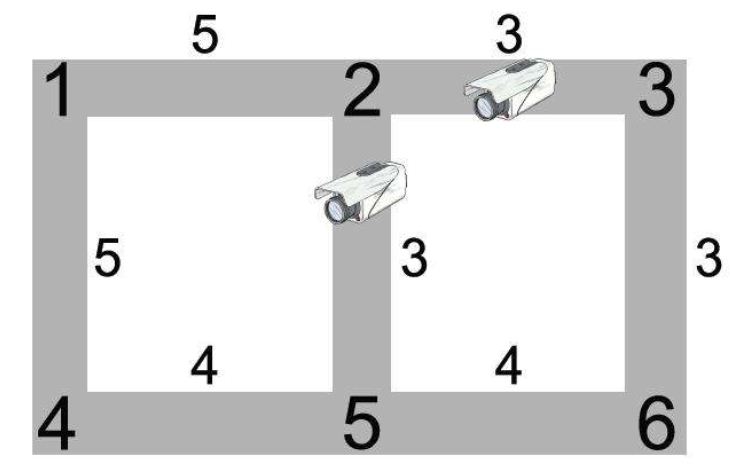
Hệ thống đường ở Singapore có thể được mô tả bởi một dãy các nút giao thông và các đường nối hai chiều (xem hình vẽ). Một vòng đua bao gồm một nút giao thông xuất phát, tiếp theo là đường đi bao gồm ít nhất 3 tuyến đường và cuối cùng quay trở lại điểm xuất phát. Trong một vòng đua, mỗi tuyến đường chỉ được đi qua đúng một lần, theo đúng một hướng.

Chi phí để đặt camera phụ thuộc vào tuyến đường được chọn. Các số nhỏ trong hình vẽ cho biết chi phí để đặt camera lên các tuyến đường. Các số lớn xác định các nút giao thông. Camera được đặt trên các tuyến đường chứ không phải tại các nút giao thông. Bạn cần chọn một số tuyến đường sao cho chi phí lắp đặt là thấp nhất đồng thời vẫn đảm bảo có ít nhất một camera dọc theo mỗi vòng đua.

Viết chương trính tìm cách đặt các camera theo dõi giao thông sao cho tổng chi phí lắp đặt là thấp nhất.

Dữ liệu

• Dòng đầu tiên chứa 2 số nguyên n, m ( 1 ≤ n ≤ 10000, 1 ≤ m ≤ 100000) là số nút giao thông và số đường nối. Các nút giao thông được đánh số từ 1 đến n.
• m dòng tiếp theo mô tả các đường nối, mỗi dòng bao gồm 3 số nguyên dương cho biết hai đầu mút của tuyến đường và chi phí lắp đặt camera. Chi phí lắp đặt thuộc phạm vi [1, 1000].

Kết qủa

In ra 1 số nguyên duy nhất là tổng chi phí lắp đặt thất nhất tìm được.

Ví dụ

**Dữ liệu:**
6 7
1 2 5
2 3 3
1 4 5
4 5 4
5 6 4
6 3 3
5 2 3

**Kết qủa**
6