Một hệ thống gồm n máy tính đánh số từ 1 đến n được kết nối thành một mạng bởi m đoạn cáp mạng đánh số từ 1 đến m. Đoạn cáp mạng thứ i có thông lượng wi kết nối hai máy ui, vi cho phép truyền dữ liệu theo cả hai chiều giữa hai máy này.

Một dãy các máy x1, x2, …, xp trong đó giữa hai máy xj và xj+1 (j = 1, 2, …, p-1) có đoạn cáp nối được gọi là một đường truyền tin từ máy x1 tới máy xp. Thông lượng của đường truyền tin được xác định như là thông lượng nhỏ nhất trong số các thông lượng của các đoạn cáp mạng trên đường truyền. Giả thiết là mạng được kết nối sao cho có đường truyền tin giữa hai máy bất kì và giữa hai máy có không quá một đoạn cáp mạng nối chúng.

Người ta muốn nâng cấp mạng bằng cách tăng thông lượng của một số đoạn cáp nối trong mạng. Để tăng thông lượng của mỗi đoạn cáp mạng thêm một lượng d (d > 0) ta phải trả một chi phí đúng bằng d. Việc nâng cấp mạng phải đảm bảo là sau khi hoàn tất, thông lượng của mỗi đoạn cáp mạng i đều bằng thông lượng của đường truyền tin có thông lượng lớn nhất từ máy ui tới máy vi.

Yêu cầu: Tìm phương án nâng cấp các đoạn cáp mạng sao cho tổng chi phí nâng cấp là nhỏ nhất.

Dữ liệu:

• Dòng thứ nhất: Chứa hai số nguyên dương n, m (n, m <= 10^5).
• Dòng thứ i trong số m dòng tiếp theo chứa ba số nguyên dương ui, vi, wi (wi <= 10^6), i = 1, 2, …, m.

Các số trên cùng một dòng được ghi cách nhau ít nhất một dấu cách.

Kết quả:

Ghi ra một số nguyên duy nhất là tổng chi phí nâng cấp theo phương án tìm được.

Ví dụ:

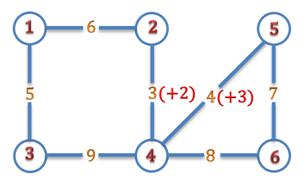
Input
6 7  
1 2 6  
1 3 5  
2 4 3  
3 4 9  
4 5 4  
4 6 8  
5 6 7

Output
5

Ràng buộc: 50% số test ứng với 50% số điểm của bài có n <= 100.