Problem
https://vn.spoj.com/problems/WEATHER
https://oj.vnoi.info/problem/WEATHER
Hãng hàng không OlympAirways thực hiện các chuyến bay giữa n sân bay được đánh số từ 1 đến n. Hệ thống các chuyến bay được thiết lập sao cho giữa 2 sân bay bất kỳ được phục vụ bởi hãng luôn có một đường bay bao gồm một hoặc nhiều chuyến bay trực tiếp giữa hai sân bay. Mỗi chuyến bay thực hiện việc di chuyển giữa hai thành phố theo cả hai chiều.
Trung tâm điều khiển của hãng đưa ra khái niệm độ dính kết giữa cặp hai sân bay A và B được xác định như là số lượng các chuyến bay mà việc không thực hiện một trong số chúng (các chuyến bay khác vẫn thực hiện bình thường) dẫn đến không thể bay từ sân bay A đến sân bay B.
Một nghiên cứu cho biết rằng, trong điều kiện thời tiết xấu, tổng độ dính kết giữa các cặp sân bay phải đạt đến một giá trị nhất định thì hệ thống đường bay mới được gọi là an toàn.
Yêu cầu: Hãy giúp trung tâm điều khiển tính tổng độ dính kết giữa mọi cặp sân bay.
Dữ liệu
- Dòng đầu tiên chứa số nguyên
n (1 ≤ n ≤ 100) - Dòng thứ hai chứa số nguyên
m (1 ≤ m ≤ 5,000) - số lượng các chuyến bay - Mỗi dòng trong số
m dòng tiếp theo chứa thông tin về một chuyến bay, bao gồm hai số nguyên dương trong khoảng từ 1 đến n: chỉ số của hai sân bay được nối bởi chuyến bay.
Kết quả
In ra 1 số nguyên duy nhất là tổng độ dính kết giữa mọi cặp sân bay (A, B) (với A < B).
Ví dụ
Input
5
5
1 2
4 2
4 5
3 2
3 1
Output
10
Tutorial
Gợi ý: sử dụng giải thuật Tarjan.
Dễ thấy với mỗi cặp đỉnh (u,v) ta chỉ quan tâm các cạnh là cầu của đồ thị, xem từ u có thể đến được v mà cần qua bao nhiêu cầu. Với mỗi cầu của đồ thị, gọi là (u,v) với u là cha của v, số cặp đỉnh cần qua cầu này là f[v] * (n - f[v]) với f[v] là số đỉnh trong cây DFS gốc v. Dễ thấy công thưc trên, minh họa bằng hình sau:
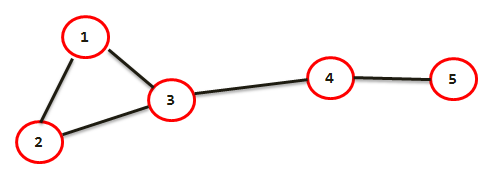
Hình trên (3,4) là cầu, số cặp lúc đó là 3*2. (f[4] = 2, 4 là con 3)
Còn tính f[u] chỉ đơn giản bằng QHĐ trong lúc DFS.
Độ phức tạp O(N+M).
Submission
Nếu bạn thấy bài viết này hay, hãy share bài viết này cho mọi người nhé 😉.
Share this post → 