Để truy bắt tội phạm, cảnh sát xây dựng một hệ thống máy tính mới. Bản đồ khu vực bao gồm N thành phố và E đường nối 2 chiều. Các thành phố được đánh số từ 1 đến N.
Cảnh sát muốn bắt các tội phạm di chuyển từ thành phố này đến thành phố khác. Các điều tra viên, theo dõi bản đồ, phải xác định vị trí thiết lập trạm gác. Hệ thống máy tính mới phải trả lời được 2 loại truy vấn sau:
- Đối với hai thành phố A, B và một đường nối giữa hai thành phố G1, G2, hỏi tội phạm có thể di chuyển từ A đến B nếu đường nối này bị chặn (nghĩa là tên tội phạm không thể sử dụng con đường này) không?
- Đối với 3 thành phố A, B, C, hỏi tội phạm có thể di chuyển từ A đến B nếu như toàn bộ thành phố C bị kiểm soát (nghĩa là tên tội phạm không thể đi vào thành phố này) không?
Dữ liệu vào
- Dòng đầu tiên chứa 2 số nguyên
N và E (2 ≤ N ≤ 100,000, 1 ≤ E ≤ 500,000), số thành phố và số đường nối. - Mỗi dòng trong số
E dòng tiếp theo chứa 2 số nguyên phân biệt thuộc phạm vi [1, N] - cho biết nhãn của hai thành phố nối với nhau bởi một con đường. Giữa hai thành phố có nhiều nhất một đường nối. - Dòng tiếp theo chứa số nguyên
Q (1 ≤ Q ≤ 300,000), số truy vấn được thử nghiệm trên hệ thống. - Mỗi dòng trong
Q dòng tiếp theo chứa 4 hoặc 5 số nguyên. Số đầu tiên cho biết loại truy vấn - 1 hoặc 2.- Nếu loại truy vấn là 1, tiếp theo trên cùng dòng là 4 số nguyên
A, B, G1, G2 với ý nghĩa như đã mô tả. A khác B; G1, G2 mô tả một con đường có sẵn. - Nếu loại truy vấn là 2, tiếp theo trên cùng dòng là 3 số nguyên
A, B, C với ý nghĩa như đã mô tả. A, B, C đôi một khác nhau.
Dữ liệu được cho sao cho ban đầu luôn có cách di chuyển giữa hai thành phố bất kỳ.
Kết quả
Gồm Q dòng, mỗi dòng chứa câu trả lời cho một truy vấn. Nếu câu trả lời là khẳng định, in ra yes. Nếu câu trả lời là phủ định, in ra no.
Ví dụ
Input
13 15
1 2
2 3
3 5
2 4
4 6
2 6
1 4
1 7
7 8
7 9
7 10
8 11
8 12
9 12
12 13
5
1 5 13 1 2
1 6 2 1 4
1 13 6 7 8
2 13 6 7
2 13 6 8
Output
yes
yes
yes
no
yes
Nhận xét: đồ thị liên thông.
Lấy ý tưởng từ giải thuật Tarjan, DFS từ 1 đỉnh trên đồ thị, lưu lại thứ tự duyệt đỉnh num[u] và đỉnh thấp nhất trên đường đi mà đỉnh u đến quay về được low[u] (low link).
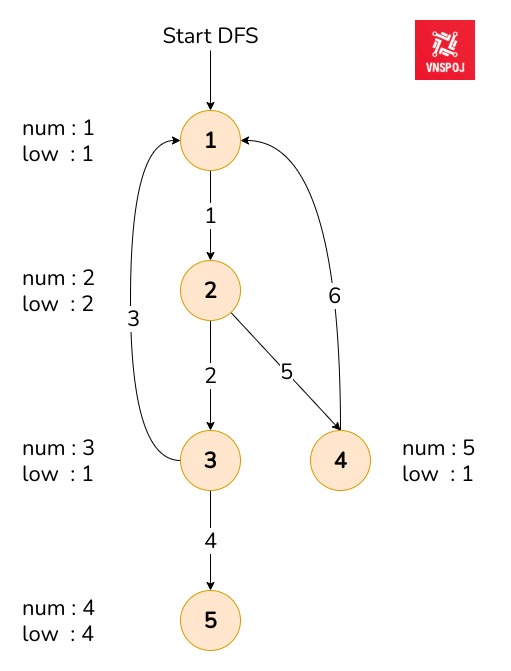
Truy vấn 1: A, B, G1, G2
Đối với truy vấn này, cần kiểm tra tính liên thông từ A đến B trên đồ thị không chứa cạnh (G1,G2). Giả sử trên đường đi duyệt DFS ở trên, G1 duyệt trước G2 (num[G1] < num[G2]), có 2 trường hợp xảy ra:
G1 không phải là cha trực tiếp của G2 trong lúc duyệt DFS: tức tồn tại đường đi từ G1 đến G2 không đi qua cạnh (G1,G2), do đó nếu xóa cạnh này thì tính liên thông đồ thị không thay đổi ==> A liên thông với B.

G1 là cha trực tiếp của G2 trong lúc duyệt DFS: trong trường hợp này, nếu từ G2 có đường đi ngược lên các node thấp hơn G1 thì tính liên thông đồ thị không đổi (low[G2] <= num[G1]).
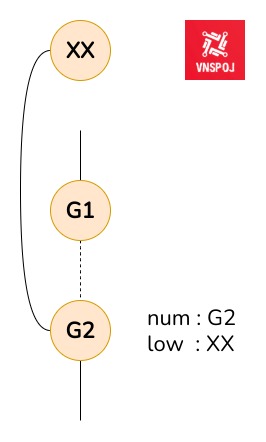
Sau cùng cần kiểm tra vị trí A và B so với G2, đảm bảo rằng cả 2 cùng thuộc hoặc ko thuộc cây gốc G2.

Truy vấn 2: A, B, C
Giả sử A được duyệt trước B trong quá trình DFS (num[A] < num[B]).
Xét trường hợp A,B là 1 cạnh trực tiếp của đồ thị (A là cha trực tiếp của B).
Xét trường hợp B được duyệt trong cây gốc A và ngược lại.
Ở từng trường hợp, cần kiểm tra vị trí của C với A, B, kiểm tra cha chung và low link giữa các node.
Nếu bạn thấy bài viết này hay, hãy share bài viết này cho mọi người nhé 😉.
Share this post → 


