Nhận thấy n lẻ không có cách xếp (dễ thấy điều này khi diện tích cần lắp là số lẻ, trong khi diện tích các viên gạch luôn chẵn).

Với n chẵn. Gọi F[i] là số cách lắp 3*i. F[0] = 1; F[2] = 3;

Bây giờ tính số cách hình thành cột i. Nhìn hình :

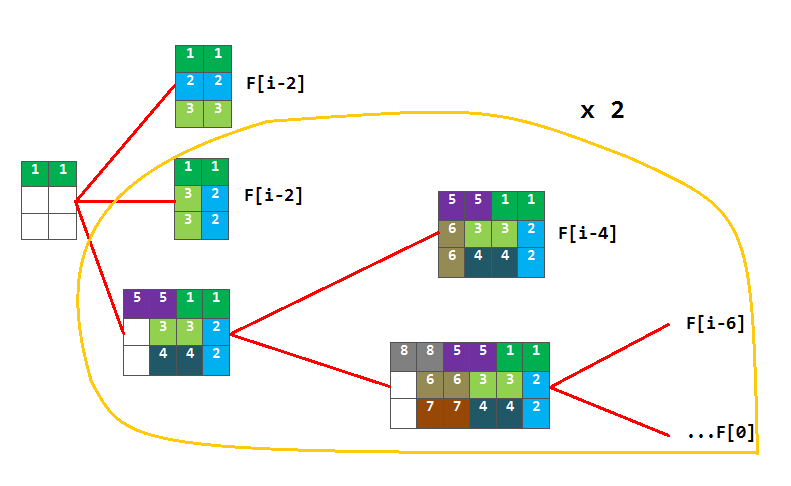
Do đó ta thấy khi lắp lần lượt vào thì lại sinh ra rất nhiều cách cho đến khi không còn ô nữa, trong đó F[i-2] có một trường hợp riêng rẽ, còn lại (phần khoanh tròn màu cam) vị lặp lại hai lần (dựa vào việc đặt viên 1-1 trên hay dưới). Do đó F[i] = F[i-2] + 2(F[i-2]+F[i-4]+…+F[0]).

Có thể tối ưu công thức trên bằng phần bù chăng, các bạn thử suy nghĩ xem ? (trong trường hợp N lớn bắt buộc dùng O(N), các bạn có thể lưu biến lưu dữa giá trị tổng F trước đó, thì chỉ cần O(1). Còn phần bù mình nói thì các bạn thử nha.)