Given an array A[0..N-1]. For each query of the form [L, R] we want to find the minimum in the array A starting from position L and ending with position R. We will assume that the array A doesn’t change in the process, i.e. this article describes a solution to the static RMQ problem

Here is a description of an asymptotically optimal solution. It stands apart from other solutions for the RMQ problem, since it is very different from them: it reduces the RMQ problem to the LCA problem, and then uses the Farach-Colton and Bender algorithm, which reduces the LCA problem back to a specialized RMQ problem and solves that.

Algorithm

We construct a Cartesian tree from the array A. A Cartesian tree of an array A is a binary tree with the min-heap property (the value of parent node has to be smaller or equal than the value of its children) such that the in-order traversal of the tree visits the nodes in the same order as they are in the array A.

In other words, a Cartesian tree is a recursive data structure. The array A will be partitioned into 3 parts: the prefix of the array up to the minimum, the minimum, and the remaining suffix. The root of the tree will be a node corresponding to the minimum element of the array A, the left subtree will be the Cartesian tree of the prefix, and the right subtree will be a Cartesian tree of the suffix.

In the following image you can see one array of length 10 and the corresponding Cartesian tree.

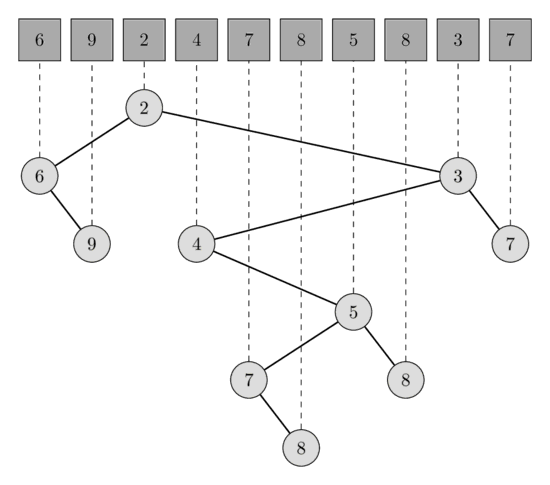
The range minimum query [l, r] is equivalent to the lowest common ancestor query [l', r'], where l' is the node corresponding to the element A[l] and r' the node corresponding to the element A[r]. Indeed the node corresponding to the smallest element in the range has to be an ancestor of all nodes in the range, therefor also from l' and r'. This automatically follows from the min-heap property. And is also has to be the lowest ancestor, because otherwise l' and r' would be both in the left or in the right subtree, which generates a contradiction since in such a case the minimum wouldn’t even be in the range.

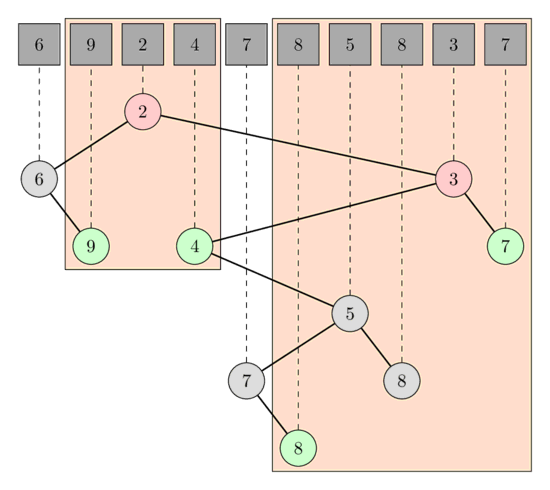
In the following image you can see the LCA queries for the RMQ queries [1, 3] and [5, 9]. In the first query the LCA of the nodes A[1] and A[3] is the node corresponding to A[2] which has the value 2, and in the second query the LCA of A[5] and A[9] is the node corresponding to A[8] which has the value 3.

Such a tree can be built in $O(N)$ time and the Farach-Colton and Benders algorithm can preprocess the tree in $O(N)$ and find the LCA in $O(1)$.

Construction of a Cartesian tree

We will build the Cartesian tree by adding the elements one after another. In each step we maintain a valid Cartesian tree of all the processed elements. It is easy to see, that adding an element s[i] can only change the nodes in the most right path - starting at the root and repeatedly taking the right child - of the tree. The subtree of the node with the smallest, but greater or equal than s[i], value becomes the left subtree of s[i], and the tree with root s[i] will become the new right subtree of the node with the biggest, but smaller than s[i] value.

This can be implemented by using a stack to store the indices of the most right nodes.

vector<int> parent(n, -1);
stack<int> s;
for (int i = 0; i < n; i++) {
    int last = -1;
    while (!s.empty() && A[s.top()] >= A[i]) {
        last = s.top();
        s.pop();
    }
    if (!s.empty())
        parent[i] = s.top();
    if (last >= 0)
        parent[last] = i;
    s.push(i);
}